数学を学んでいると、「実数」とか「自然数」とか「整数」とかいう単語を目にする機会がよくあると思います。
これらはいずれも数を種類分けする際に利用する単語であり、とても有用なのですが、実は高校生でも正確に意味を理解してこれらの単語を使いこなしている人は少ないのが実情だと思います。
本記事では以下の数学用語について、できるだけわかりやすく解説します。
本記事で解説している数学用語
・実数
・有理数/無理数
・正の整数（=自然数）/負の整数
・有限小数/無限小数
他にも数を種類分けする単語は存在しますが、中学範囲では上の4種類で十分だと思いますので、ここでは割愛します。
見出し
■まずは結論！実数・自然数等の関係性まとめ！
細かな説明に入る前に、まずは図で視覚的にグループ分けを見てみましょう！
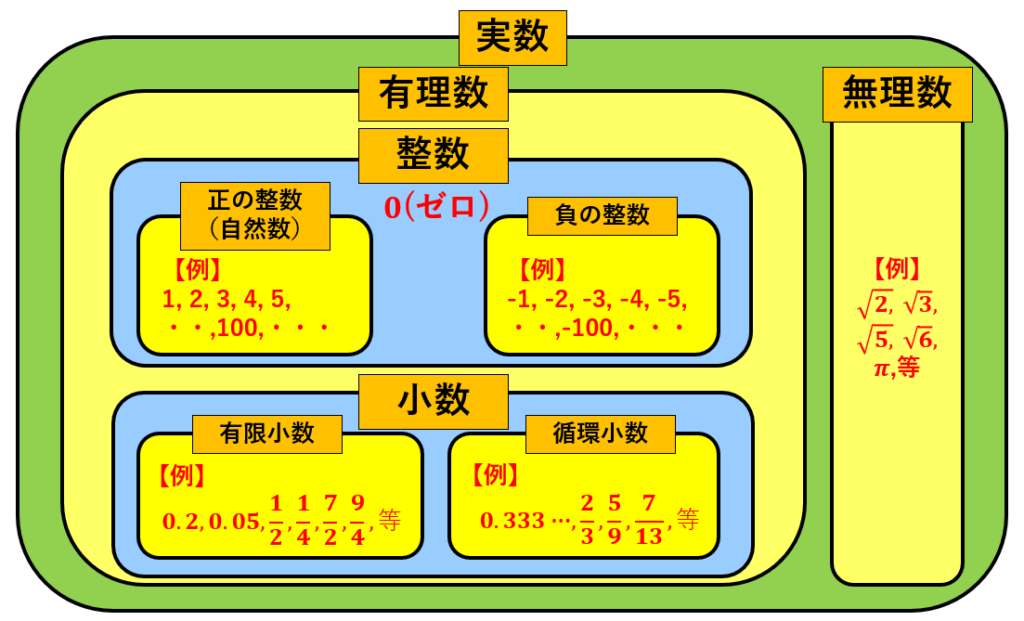
まず中学生の段階で出てくる数字は全て「実数」の範囲内に含まれています。
次に、実数の中で「有理数」と「無理数」に分類されます。
そして、有理数の中では「整数」、「小数」に分類され、その2種はさらに分類される、、、みたいな感じです。
例としまして、【-50】という数字があったとすると、この数字は「実数」、「有理数」、「整数」、「負の整数」のいずれのグループにも所属している数字、ということになります。
ちなみに【0】は、「整数」ではあるのですが、「正の整数」にも「負の整数」にも所属しない、特殊な数字となります。
※他の整数は必ず「正の整数」か「負の整数」のいずれかに分類されます。
■実数って何？
上の図からわかるように、まず中学生の範囲で学ぶ数字は全て「実数」というものになります。
高校数学になると、実数の対として「虚数」というものが出てきます。
中学生は学ぶ必要はないですが、気になる方は是非ググってみて下さい！
■有理数/無理数って何？
有理数/無理数のグループ分けは実は簡単です。
ズバリ、分母分子が整数の分数で表すことができる数が「有理数」、できない数が「無理数」となります。
例えば「整数」は全て、分母を1とした分数で表すことができるので、「有理数」に含まれます。
一方、\(\displaystyle \sqrt{2}\) や\(\displaystyle \sqrt{3}\)、\(\displaystyle \pi\)についてはどう頑張っても分母分子を整数とした分数では表すことができないため、これらは「無理数」となるわけです。
■整数/自然数って何？
まずは理解しやすい「自然数」から理解しましょう。
簡単に言うと、物の個数を数えたり、順番を数えたりする際に使用する数字が「自然数」です。
数を数える時、指を折って「1,2,3,4,5,,,,」と数えると思います。
この数を数える時に利用する数が「自然数」です。
また、自然数は「正の整数」と表現されることもありますが、どちらも同じ意味となりますので、惑わされることがないようにしましょう。
一方、自然数にマイナスをつけた数は「負の整数」と定義されます。
■（補足1）「整数」≠「正数」であることに注意！
実はここでは説明していない数の種別用語として、「正数」というものがあります。
この用語の意味としては単純に「正の数（つまり、負の数でも0の数でもない）」という意味ですが、よく「整数」と混同してしまう人がいます。
読み方は同じなのですが、意味としてはまるで別となるので、気を付けてください！！
■有限小数/循環小数って何？
★注意★
本記事では「分数」と「小数」の区別化は特に行っておりません。
※表現方法の違いなだけであると認識しているため。
そのため、以下の「有限小数」と「循環小数」の定義説明の中で分数が含まれてしまっておりますが、これは「分数を小数に変換したときの小数の定義のことを言っている」ものとご理解ください。
「有限小数」とは、「無限に続かない小数で表現可能な分数or小数のこと」です。
例えば小数の\(0.02\)とかは当然「有限小数」です。
では、\(\displaystyle \frac{1}{2}\) はどうでしょうか。
これは小数で表現すると\(0.5\)と表現されるため、「有限小数」となります。
では、\(\displaystyle \frac{1}{3}\) はどうでしょうか。
これは小数で表すと\(0.33333333・・・\)となり、無限に3が続く形の小数になるので、「有限小数」とはなりません。
\(\displaystyle \frac{1}{3}\) のように、「途中から同じ数字の列を繰り返す形の分数or小数」は「循環小数」と定義されます。
■（補足2）整数・自然数の定義を知っていることのメリット
ここで補足として、整数・自然数を知っていることのメリットを少し紹介します。
例えば、以下のような問題があったとします。
この問題の回答として、\(x=0, 2\) と答えた方は×（甘めに見て△）です。
なぜなら、求めるように言われているのは「自然数\(x\)の値」のため、\(x=0\) の値を答えると減点or間違いとなります。
※\(x=0\) は自然数ではないため。
つまり、上記例題の回答としては \(x=2\) だけが正解となります。
このように、「自然数」や「整数」の正確な定義を理解していないと、解ける問題も解けないようになってしまうわけです！
■【まとめ】”整数”と”自然数”の違いだけでも理解しておこう！
いかがでしたでしょうか。
先述しました通り、「自然数」や「整数」の正確な知識を持っていないと正確に回答ができない問題も今後出てきます。
本記事では色々な数を区別するための用語の説明をしてきましたが、全て覚えるのは難しいという方は、一旦は「自然数」や「整数」の違いだけでも覚えてもらえれば十分かと思います。
数学が得意な人ほど、このあたりの定義を正確に知っているので、是非この機会に覚えて、他の人と差をつけてしまいましょう！
最後まで本記事を読んでいただき、ありがとうございました！