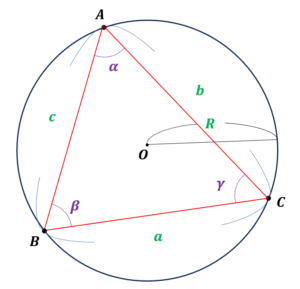
本記事では、三角関数の正弦定理・余弦定理以下の加法定理が何故成り立つのか、できるだけ丁寧にまとめてみました！
是非参考にしていただけると幸いです！
ちなみに、「正弦」とはサイン（\(\sin\)）、
「余弦」とはコサイン（\(\cos\)）のことです！
本記事で証明する正弦定理・余弦定理
■正弦定理
① \(\displaystyle \frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma} = 2R\)
② \(\displaystyle \sin \alpha : \sin \beta : \sin \gamma = a : b : c\)
■余弦定理
③ \(\displaystyle a^2 = b^2 + c^2 -2bc\cos \alpha\)
\(\displaystyle b^2 = c^2 + a^2 -2bc\cos \beta\)
\(\displaystyle c^2 = a^2 + b^2 -2bc\cos \gamma\)
※ただし、\(a,b,c\) は三角形ABCの辺の長さ、
\(\alpha,\beta,\gamma\) は三角形ABCの角度、
\(R\)は三角形ABCの外接円の半径とする。
■正弦定理①の証明
上の図を、「円周角の定理」を利用して変形すれば、正弦定理は簡単に証明できます。
まずは、直線COと外接円との交点をA'とし、三角形A'BCについて考える。
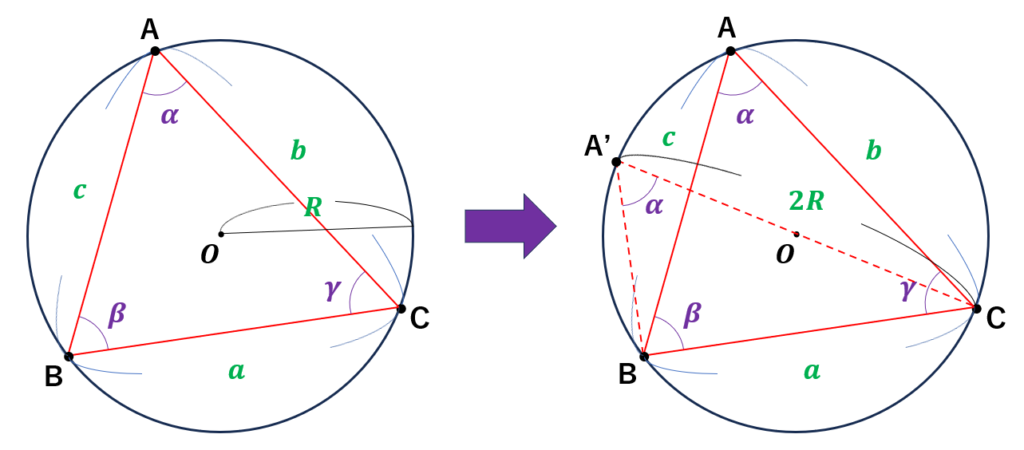
点A'を定義した際のポイント
●線分A'Cの長さは、外接円の直径となるため、A'C = \(2R\)
●「円周角の定理」より、\(\angle\) BAC = \(\angle\) BA'C = \(\alpha\)
●線分A'Cは外接円の直径であることから、\(\angle\) A'BC = \(90^{ \circ }\)
上の右図から、三角形A'BCについて考えると、三角関数の基本性質より、
\begin{equation}
\displaystyle \sin \alpha = \frac{a}{2R} \\
\unicode{x2234} \hspace{10pt} \displaystyle \frac{a}{\sin \alpha} = 2R
\end{equation}
が証明される。
同様に、\(\displaystyle \frac{b}{\sin \beta} = 2R\)、\(\displaystyle \frac{c}{\sin \gamma} = 2R\) も証明ができる。
ここまでは「鋭角三角形」の場合で証明してきました。
次は「鈍角三角形」の場合にも正弦定理が成立するのか、確認してみましょう！
角度\(\beta\)が鈍角（\(90^{ \circ } < \beta < 180^{ \circ }\)）の場合を考える。
直線AOと外接円との交点をB'とし、三角形AB'Cについて考える。
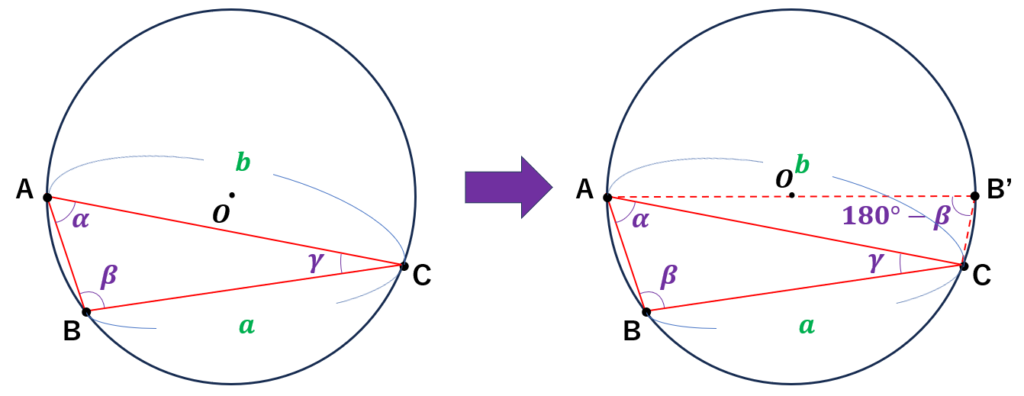
点B'を定義した際のポイント
●線分AB'の長さは、外接円の直径となるため、AB' = \(2R\)
●円に内接する四角形の体格の和が\(180^{ \circ }\)より、\(\angle\) AB'C = \(180^{ \circ }-\beta\)
●線分AB'は外接円の直径であることから、\(\angle\) ACB' = \(90^{ \circ }\)
上の右図から、三角形AB'Cについて考えると、三角関数の基本性質より、
\begin{equation}
\displaystyle \sin(180^{ \circ }-\beta) = \frac{b}{2R} \\
\unicode{x2234} \hspace{10pt} \displaystyle \frac{b}{\sin(180^{ \circ }-\beta)} = 2R \\
\unicode{x2234} \hspace{10pt} \displaystyle \frac{b}{\sin \beta} = 2R
\end{equation}
が証明される。
※ただし、最後の式変形では \(\sin(180^{ \circ }-\beta) = \sin \beta\) の関係性を利用した。
同様に、\(\displaystyle \frac{a}{\sin \alpha} = 2R\)、\(\displaystyle \frac{c}{\sin \gamma} = 2R\) も証明ができる。
■正弦定理②の証明
「正弦定理①」が証明できれば、実は既にこれについては証明できている。
\(\displaystyle \frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma} = 2R\) であるから、
\begin{equation}
\displaystyle a : \sin \alpha = 2R:1 \\
\displaystyle b : \sin \beta = 2R:1 \\
\displaystyle c : \sin \gamma = 2R:1
\end{equation}
の関係性が成立している。これら3式の比を1つの式にまとめると、
\begin{equation}
\displaystyle a : b : c = \sin \alpha : \sin \beta : \sin \gamma
\end{equation}
となり、「正弦定理②」が導ける。
■余弦定理③の証明
余弦定理も、三角形に一本の垂線を引くだけで簡単に証明できます。
まず、点Cから線分ABに垂線を引き、線分ABと交わる点をHと定義する。
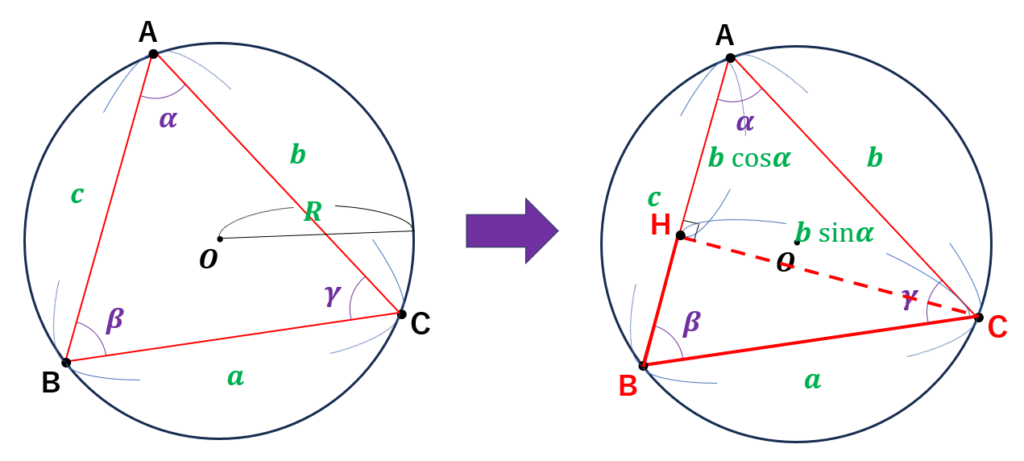
点Hを定義した際のポイント
●線分AH、CH、BHの長さは、三角関数を用いて以下と表される。
\begin{eqnarray}
\displaystyle AH &=& b\cos \alpha \\
\displaystyle CH &=& b\sin \alpha \\
\displaystyle BH &=& c - AH = c - b\cos \alpha
\end{eqnarray}
三角形BCHに対し、三平方の定理を利用して、
\begin{eqnarray}
\displaystyle BC^2 &=& CH^2 + HB^2 \\
⇒ \displaystyle a^2 &=& (b\sin\alpha)^2 + (c-b\cos\alpha)^2 \\
\displaystyle &=& b^2\sin^2\alpha + c^2-2bc\cos\alpha+b^2\cos^2\alpha \\
\displaystyle &=& b^2(\sin^2\alpha+\cos^2\alpha) + c^2-2bc\cos\alpha \\
\displaystyle &=& b^2 + c^2-2bc\cos\alpha
\end{eqnarray}
となり、「余弦定理③」が証明できる。
同様に、\(\displaystyle b^2 = c^2 + a^2 -2bc\cos \beta\)、\(\displaystyle c^2 = a^2 + b^2 -2bc\cos \gamma\) も証明ができる。
ここまでは「鋭角三角形」の場合で証明してきました。
次は「鈍角三角形」の場合にも余弦定理が成立するのか、確認してみましょう！
角度\(\beta\)が鈍角（\(90^{ \circ } < \beta < 180^{ \circ }\)）の場合を考える。
点Cから直線ABに垂線を引き、その交点をHと定義する。
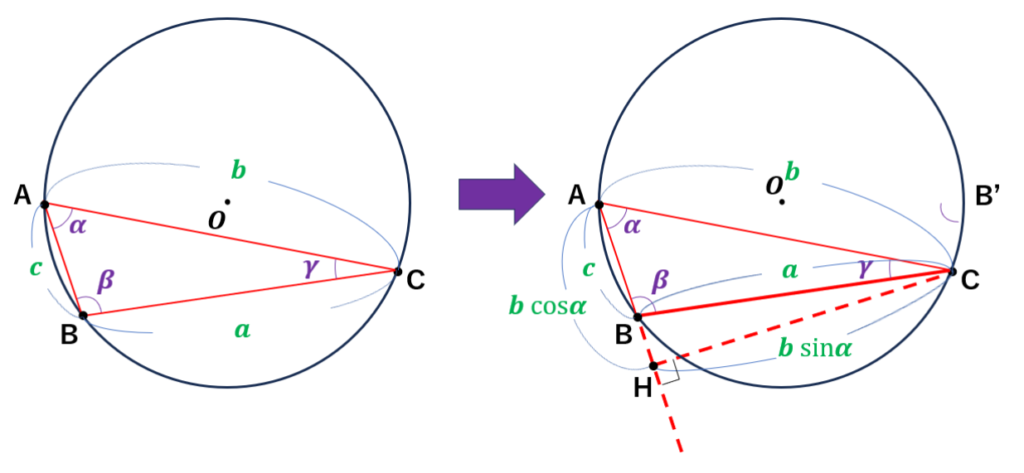
各辺の長さは上図の通りであるため、三角形BCHに対し三平方の定理を利用して、
\begin{eqnarray}
\displaystyle BC^2 &=& CH^2 + HB^2 \\
⇒ \displaystyle a^2 &=& (b\sin\alpha)^2 + (b\cos\alpha-c)^2 \\
\displaystyle &=& b^2\sin^2\alpha+b^2\cos^2\alpha-2bc\cos\alpha+c^2 \\
\displaystyle &=& b^2(\sin^2\alpha+\cos^2\alpha) + c^2-2bc\cos\alpha \\
\displaystyle &=& b^2 + c^2-2bc\cos\alpha
\end{eqnarray}
となり、鈍角三角形の場合も「余弦定理③」が証明できる。
■まとめ
いかがでしたでしょうか。
学生の方は、普段は普通に使いこなしているであろう公式だと思いますが、いざ証明するように言われると難しいかと思います。
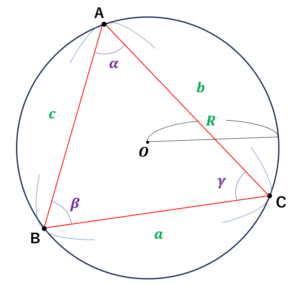
本記事を読んでいただいた方であれば、正弦定理も余弦定理も、基本的には以下の図から求められることを理解いただけたかと思いますので、
是非以下の図の形だけでも覚えていってもらえたら幸いです。（まあ特に変哲もない三角形＋外接円ですが笑）
「なぜこの公式は成立するのか？」「なぜこの公式は使っていいんだっけ？」の部分を理解しながら数学を勉強していくだけでも、
数学がとても楽しくなってくると思いますので、本記事がその一助となっていれば幸いです。
ここまで記事を読んでいただき、ありがとうございました！！