高校で学ぶ三角関数(\(\sin\), \(\cos\), \(\tan\))について、皆さんどれほど理解しておりますでしょうか。
特に理系の方でもない限り、「結局、三角関数って何だったんだ、、?」とか、「結局何に使うんだろう、、?」と思いながら、高校を卒業していく方が大半だと思います。
本記事では、そんな方向けに「三角関数の定義」~「三角関数ってどう使うの?」の部分について、可能な限り丁寧にまとめてみましたので、是非最後までお読みいただけますと幸いです!

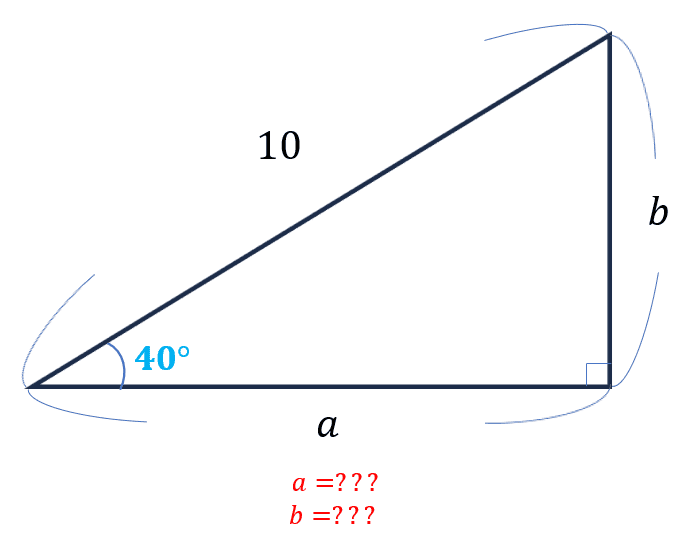
以下のような三角形を考えた際、 \(a, b\) の長さを求めたい場合などに、三角関数を利用することで求めることが可能となります!!
本記事の内容
- 三角関数(\(\sin, \cos, \tan\))って結局何なの?
- 三角関数の値はどうやって決まるの?
- 三角関数の基本公式の証明:
- \(\sin^2 \theta+\cos^2 \theta=1\)
- \(\displaystyle \frac{\sin \theta}{\cos \theta}=\tan \theta\)
- \(1+\tan^2 \theta=\displaystyle \frac{1}{\cos^2 \theta}\)
- 三角関数って何に使うの?
①三角関数の定義
図で理解するのが一番早いと思います。
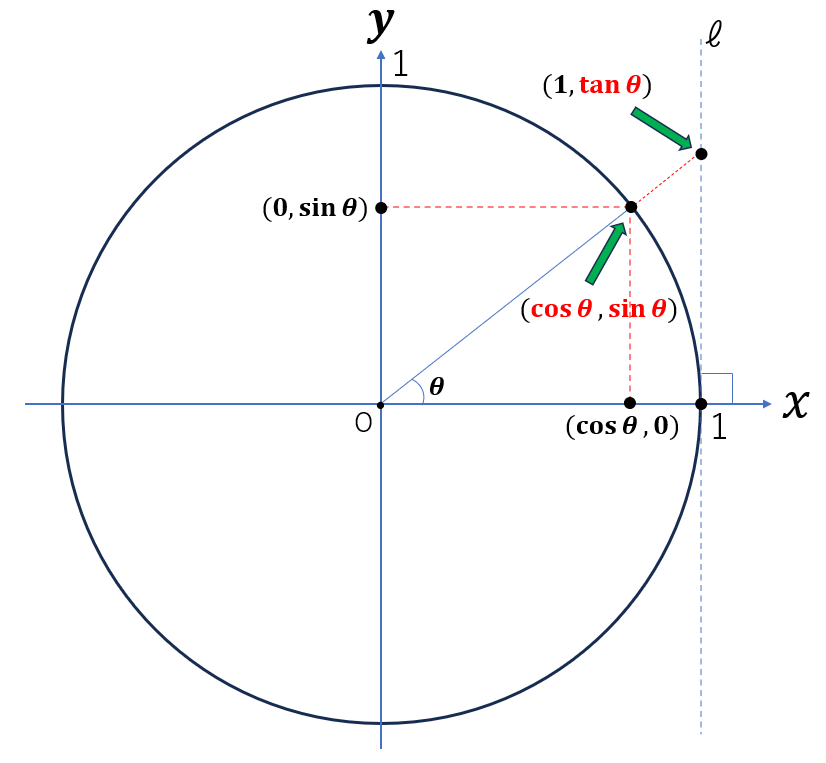
■\(\sin \theta\) の定義:
\(x\) 軸の\(x\)>0 の線から角度 \(\theta\) の方向に引いた直線と、単位円(半径が1の円)との交点の \(\color{red}{y}\) 座標
■\(\cos \theta\) の定義:
\(x\) 軸の \(x\)>0 の線から角度 \(\theta\) の方向に引いた直線と、単位円(半径が1の円)との交点の \(\color{red}{x}\) 座標
■\(\tan \theta\) の定義:
\(x\) 軸の \(x\)>0 の線から角度 \(\theta\) の方向に引いた直線と、直線 \(x=1\) との交点の \(\color{red}{y}\) 座標
②三角関数の定義域(取れる値の範囲)
上で述べた「三角関数の定義」より、\(\sin \theta\)、\(\cos \theta\)については単位円上で定義されるため、
\begin{eqnarray}
-1 \leqq \sin \theta \leqq 1 \\
-1 \leqq \cos \theta \leqq 1
\end{eqnarray}
となる。一方、\(\tan \theta\)については直線 \(x=1\) 上の点ならどこでも取れるため、
\begin{eqnarray}
-\infty \lt \tan \theta \lt \infty \\
\end{eqnarray}
となる。
③よく利用する三角関数の値
・上で述べた「三角関数の定義」より、三角関数は角度 \(\theta\) 次第で値が決定する。
・基本的に三角関数は綺麗な値にはならず、いくつかの無理数の足し算などで表される。
・しかし、比較的綺麗な値になるものも存在するため、以下表で綺麗な値になるときの角度 \(\theta\) とその時の三角関数の値をまとめておく。
| \(\sin \theta\) | \(\cos \theta\) | \(\tan \theta\) | |
| \(\theta = 0^{ \circ }\) | \(0\) | \(1\) | \(0\) |
| \(\theta = 30^{ \circ }\) | \(\cfrac{1}{2}\) | \(\cfrac{\sqrt{3}}{2}\) | \(\cfrac{\sqrt{3}}{3}\) |
| \(\theta = 45^{ \circ }\) | \(\cfrac{\sqrt{2}}{2}\) | \(\cfrac{\sqrt{2}}{2}\) | \(1\) |
| \(\theta = 60^{ \circ }\) | \(\cfrac{\sqrt{3}}{2}\) | \(\cfrac{1}{2}\) | \(\sqrt{3}\) |
| \(\theta = 90^{ \circ }\) | \(1\) | \(0\) | 未定義(※1) |
| \(\theta = 120^{ \circ }\) | \(\cfrac{\sqrt{3}}{2}\) | -\(\cfrac{1}{2}\) | -\(\sqrt{3}\) |
| \(\theta = 135^{ \circ }\) | \(\cfrac{\sqrt{2}}{2}\) | -\(\cfrac{\sqrt{2}}{2}\) | -\(1\) |
| \(\theta = 150^{ \circ }\) | \(\cfrac{1}{2}\) | -\(\cfrac{\sqrt{3}}{2}\) | -\(\cfrac{\sqrt{3}}{3}\) |
| \(\theta = 180^{ \circ }\) | \(0\) | -\(1\) | \(0\) |
| \(\theta = 210^{ \circ }\) | -\(\cfrac{1}{2}\) | -\(\cfrac{\sqrt{3}}{2}\) | \(\cfrac{\sqrt{3}}{3}\) |
| \(\theta = 225^{ \circ }\) | -\(\cfrac{\sqrt{2}}{2}\) | -\(\cfrac{\sqrt{2}}{2}\) | \(1\) |
| \(\theta = 240^{ \circ }\) | -\(\cfrac{\sqrt{3}}{2}\) | -\(\cfrac{1}{2}\) | \(\sqrt{3}\) |
| \(\theta = 270^{ \circ }\) | -\(1\) | \(0\) | 未定義(※2) |
| \(\theta = 300^{ \circ }\) | -\(\cfrac{\sqrt{3}}{2}\) | \(\cfrac{1}{2}\) | -\(\sqrt{3}\) |
| \(\theta = 315^{ \circ }\) | -\(\cfrac{\sqrt{2}}{2}\) | \(\cfrac{\sqrt{2}}{2}\) | -\(1\) |
| \(\theta = 330^{ \circ }\) | -\(\cfrac{1}{2}\) | \(\cfrac{\sqrt{3}}{2}\) | -\(\cfrac{\sqrt{3}}{3}\) |
| \(\theta = 360^{ \circ }\) | \(0\) | \(1\) | \(0\) |
(※2)このとき\(\tan\)の値は\(-\infty\)に限りなく近くなる

他の角度の値も気になる方については、「三角関数表」などでググってみてください!
④よく利用する三角関数の角度公式
- 上で述べた「①三角関数の定義」から明らかな通り、以下等式が成り立つ。
- \(\sin (-\theta)\) = \(-\sin \theta\)
- \(\cos (-\theta)\) = \(\cos \theta\)
- \(\tan (-\theta)\) = \(-\tan \theta\)
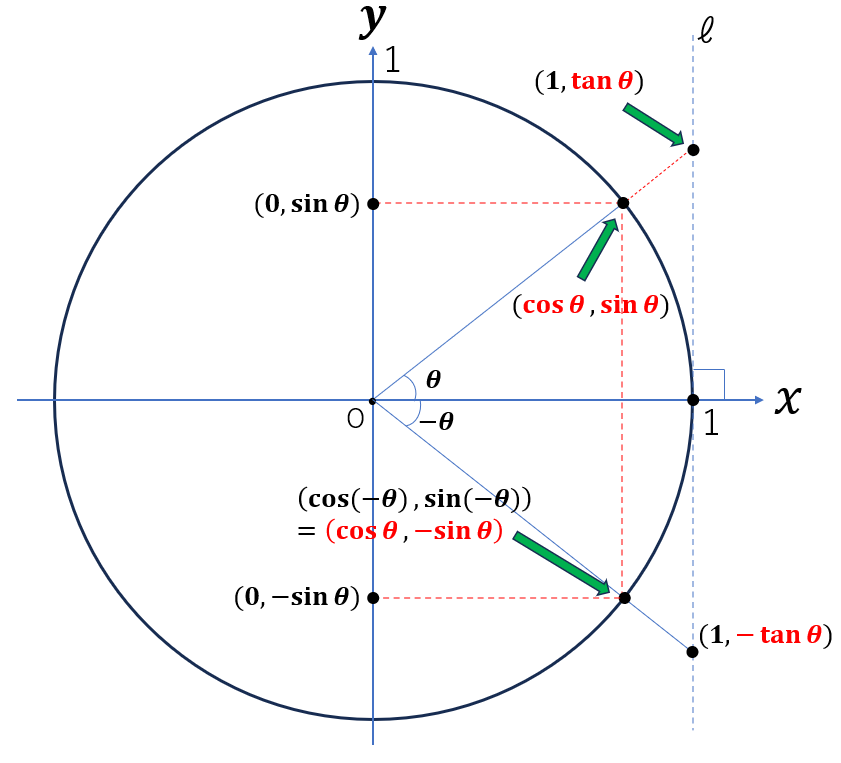
- また、\(\sin \theta\)、\(\cos \theta\) の間では以下等式が成り立つ。
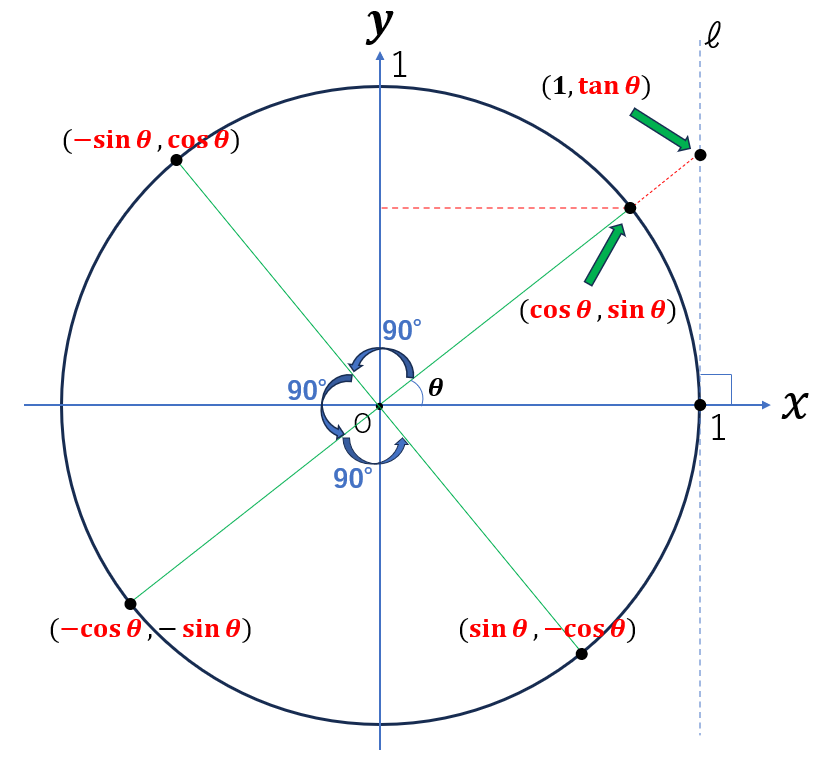
- \(\sin (\theta+90^{ \circ })\) = \(\cos \theta\)
- \(\cos (\theta+90^{ \circ })\) = \(-\sin \theta\)
- \(\sin (\theta+180^{ \circ })\) = \(-\sin \theta\)
- \(\cos (\theta+180^{ \circ })\) = \(-\cos \theta\)

上記等式が本当に合っているかどうか気になる人は、「三角関数の加法定理」を利用することで確認が可能なため、よろしければこちらの記事も参照ください!
⑤三角関数の基本公式の証明
- \(\sin \theta\)、\(\cos \theta\) 、\(\tan \theta\) の間では以下の公式が成立する。
- \(\sin^2 \theta+\cos^2 \theta=1\)
- \(\displaystyle \frac{\sin \theta}{\cos \theta}=\tan \theta\)
- \(1+\tan^2 \theta=\displaystyle \frac{1}{\cos^2 \theta}\)
- 「①三角関数の定義」で使用した図を基に、上記3つの式を証明していく。
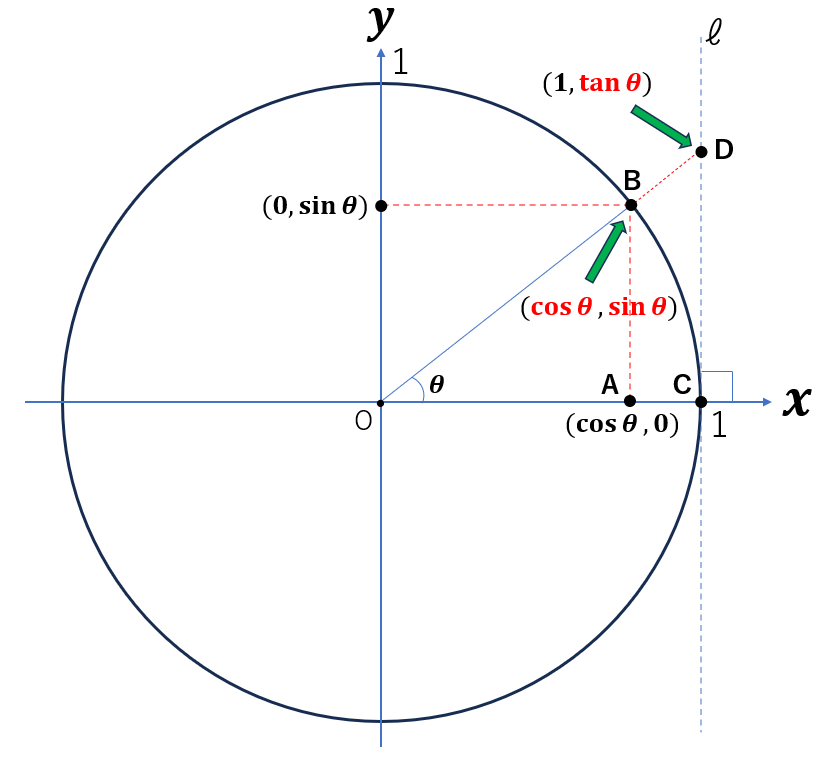
①\(\sin^2 \theta+\cos^2 \theta=1\) の証明:
\(\cos \theta\)、\(\sin \theta\) がそもそも単位円上に定義される\(x\)座標、\(y\)座標であるため、三平方の定理より上式が成立する。
②\(\displaystyle \frac{\sin \theta}{\cos \theta}=\tan \theta\) の証明:
上図において、三角形OABと三角形OCDの相似関係に着目する。
OA:AB=OC:CDより、
\begin{eqnarray}
\displaystyle \cos \theta : \sin \theta &=& 1 : \tan \theta \\
⇒ \displaystyle \cos \theta \tan \theta &=& \sin \theta \\
⇒ \tan \theta &=& \displaystyle \frac{\sin \theta}{\cos \theta} \\
\end{eqnarray}
となり、上式が成立する。
③\(1+\tan^2 \theta=\displaystyle \frac{1}{\cos^2 \theta}\) の証明:
これも実は簡単で、①式の両辺を\(\cos^2 \theta\)で割って、②式を利用すれば③式を得ることができる。
⑥結局、三角関数って何に使うの?
さあ、いよいよ本題です。
実は直角三角形の各辺と三角関数の間には、以下関係性が存在しています。
(※この関係性はメチャクチャ使いますので、是非覚えておきましょう)
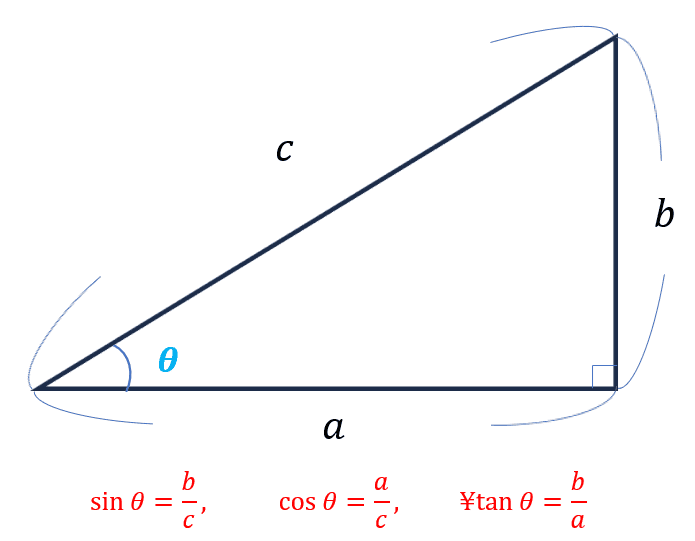
証明は簡単で、上で\(\displaystyle \frac{\sin \theta}{\cos \theta}=\tan \theta\)を証明した時と同様に、相似比を利用します。
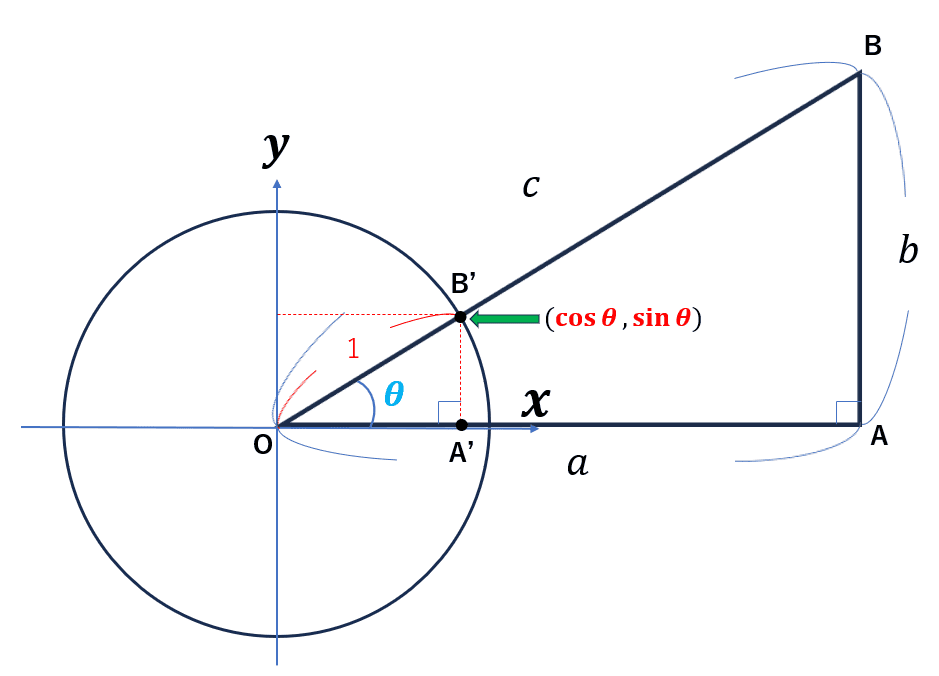
例えば三角形OABと三角形OA'B'の相似関係に着目します。
OB:BA=OB':B'A'より、
\begin{eqnarray}
c : b &=& 1 : \sin \theta \\
⇒ c \times \sin \theta &=& b \\
⇒ \sin \theta &=& \displaystyle \frac{b}{c} \\
\end{eqnarray}
同じように、\(\cos \theta = \displaystyle \frac{a}{c}\)、\(\tan \theta = \displaystyle \frac{b}{a}\)も求められるが、ここでは割愛します。
是非、手を動かして一度導出してみてください。
前置きが長くなりましたが、三角関数を知っていることで、
直角三角形の角度と1辺の長さが分かれば、他の辺の長さも求めることができるようになります。
例として、斜辺の長さが10、1つの角度が40°の直角三角形の各辺を求めてみると、
\(\sin \theta = \displaystyle \frac{b}{c}\)、\(\cos \theta = \displaystyle \frac{a}{c}\)を利用して、以下のように求められます。
※\(\sin 40^{ \circ }\), \(\cos 40^{ \circ }\) の値については、以下を確認した値を使用しました。
<https://www.math.s.chiba-u.ac.jp/~yasuda/sysKOU/cit-H20/trig-table.pdf>
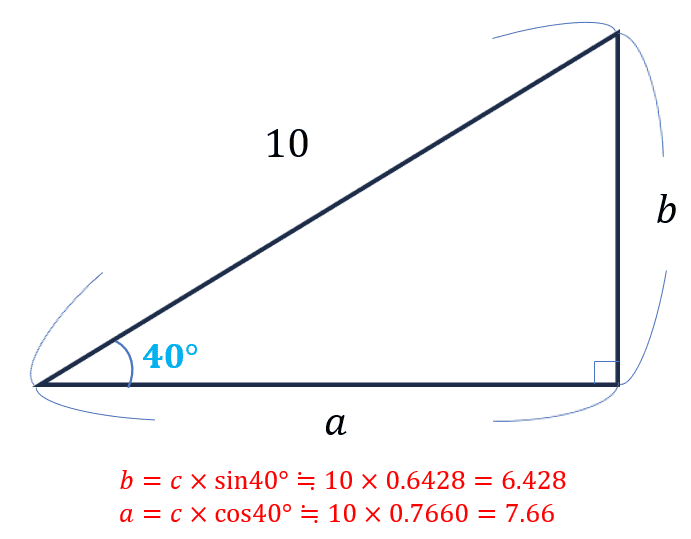
上の例は斜辺の長さが判明しているパターンでしたが、斜辺以外の1辺の長さが判明している場合でも、三角関数を利用することで他の2辺の長さを求めることができます!是非試してみてください!
★まとめ★
いかがでしたでしょうか。
上の例では、各角度がそれぞれ [\(90^{ \circ }, 40^{ \circ }, 50^{ \circ }\)] の三角形を考えましたが、もちろん他の角度の場合でも、1辺の長さが定まっていれば、三角関数を利用して残りの辺の長さを求めることができます。
現実世界では三角関数を利用して、建物の高さや物体までの距離を測定したりしていますので、社会人になっても三角関数を利用する場面は多々出てきます。そういった意味でも、ここで得た知識は決して無駄にならないかなと思っております。
本記事が少しでも皆様のお役に立っていれば幸いです。
ここまで記事を読んでいただき、ありがとうございました!
