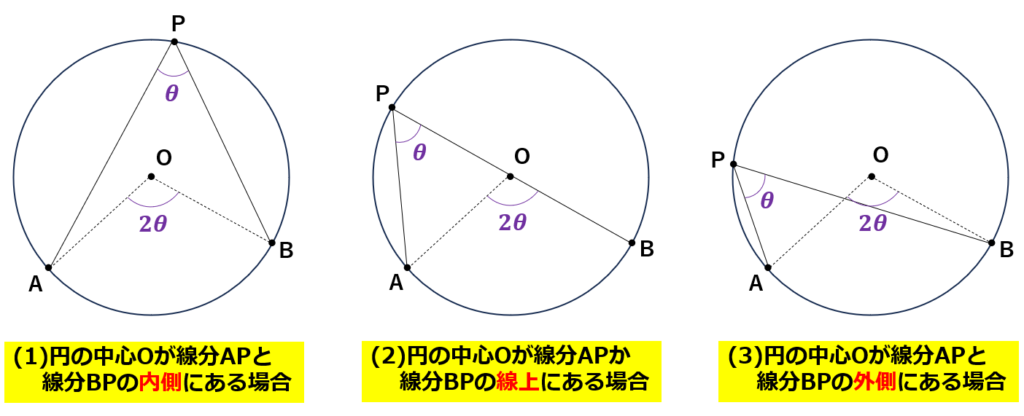
本記事では、皆さんが普段から使いこなしている「円周角の定理」が何故成り立つのか、できるだけ丁寧にまとめてみました!
是非参考にしていただけると幸いです!

(1),(2)は簡単ですが、(3)が少々難しい、、、かも?
(1)円の中心Oが線分APと線分BPの内側にある場合
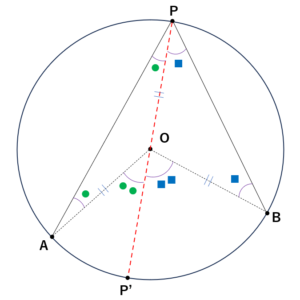
(1)の場合については、以下手順に従い証明ができます。
※証明したいのは【\(\angle AOB = 2 \times \angle APB\)】です。
(1)の証明手順
①点Pから円の中心Oに向けて直線を引き、円と交わる点をP'とする。
②三角形APOについて考える。三角形APOは二等辺三角形なので、
\begin{eqnarray}
\angle APO = \angle OAP
\end{eqnarray}
が成立する。
③「②」より、三角形APOの外角AOP'は、角APOを用いて表すと、
\begin{eqnarray}
\angle AOP' &=& \angle APO + \angle OAP \\
&=& \angle APO + \angle APO \\
&=& 2 \times \angle APO \tag{1}
\end{eqnarray}
の関係性が成立する。
④同様に、三角形BPOについても「②」「③」の考え方を適用すると、
\begin{eqnarray}
\angle BOP' &=& \angle BPO + \angle OBP \\
&=& \angle BPO + \angle BPO \\
&=& 2 \times \angle BPO \tag{2}
\end{eqnarray}
の関係性が成立することがわかる。
⑤(1)式と(2)式の両辺同士を足し合わせると、
\begin{eqnarray}
\angle AOP' + \angle BOP' &=& 2 \times \angle APO + 2 \times \angle BPO \\
&=& 2 (\angle APO + \angle BPO) \tag{3} \\
\end{eqnarray}
⑥上図より、(3)式の中で
\begin{eqnarray}
\angle AOP' + \angle BOP' = \angle AOB \\
\angle APO + \angle BPO = \angle APB
\end{eqnarray}
が成立していることが明らかなため、これより証明したい式
\begin{eqnarray}
\angle AOB = 2 \times \angle APB \\
\end{eqnarray}
を得る。
(2)円の中心Oが線分APか線分BPの線上にある場合
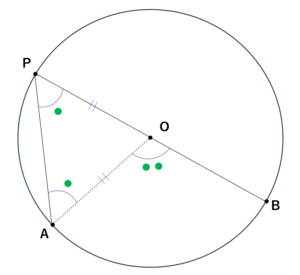
この場合は上図の通り、二等辺三角形OPAの外角を考えると、
\begin{eqnarray}
\angle AOB &=& \angle APB + \angle OAP \\
&=& \angle APB + \angle APB \\
&=& 2 \times \angle APB
\end{eqnarray}
が容易に証明できる。
(3)円の中心Oが線分APと線分BPの外側にある場合
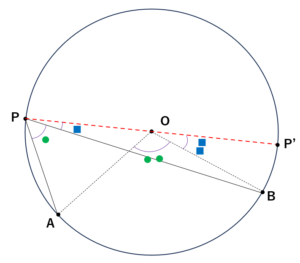
(3)の場合については、以下手順に従い証明ができます。
※おさらいですが、証明したいのは【\(\angle AOB = 2 \times \angle APB\)】です。
(3)の証明手順
①点Pから円の中心Oに向けて直線を引き、円と交わる点をP'とする。
②先ほど証明した「(2)の場合」より、弧BP'について以下が成立する。
\begin{eqnarray}
\angle BOP' = 2 \times \angle BPO \tag{4} \\
\end{eqnarray}
③また、先ほど証明した「(2)の場合」より、弧AP'について以下が成立する。
\begin{eqnarray}
\angle AOP' = 2 \times \angle APO \tag{5} \\
\end{eqnarray}
④(5)式の両辺から(4)式を引くと、
\begin{eqnarray}
\angle AOP' - \angle BOP' = 2 (\angle APO - \angle BPO) \tag{6}
\end{eqnarray}
⑤上図より、(6)式の中で
\begin{eqnarray}
\angle AOP' - \angle BOP' = \angle AOB \\
\angle APO - \angle BPO = \angle APB
\end{eqnarray}
が成立していることが明らかなため、これより証明したい式
\begin{eqnarray}
\angle AOB = 2 \times \angle APB \\
\end{eqnarray}
を得る。
まとめ
私もこの「円周角の定理」自体は覚えていて、学生時代は普通に使いこなしていましたが、いざ証明するとなったら多分、、、できませんでしたね。(笑)
特に(3)の場合の証明とかは、パッとは出てこなかったと思います。
ただまあ本来はこういった証明が完璧にできた上で使いこなすものかとも思いますので、改めて、勉強になりました。
本記事が皆様にとって少しでも参考になれば幸いです!最後までお読みいただき、ありがとうございました!