本記事では、大学数学で学ぶ「マクローリン展開」の考え方について、高校生でも理解できるように解説していきます。
また、そこからあの有名な「オイラーの公式」についても導出できるため、是非最後まで読んでいただけると幸いです!

「マクローリン展開についてよくわからない、、、」と悩んでいる大学生の方も、この記事を読めば考え方はわかるようになるはずです!
■マクローリン展開ってそもそも何?
まず最初に、マクローリン展開のそもそもの目的・考え方を述べます。
それはズバリ、三角関数、指数関数、自然対数等の関数を、\(x\)のべき乗で表現することです。
※マクローリン展開の正確な定義については、wikipedia等を参照下さい。
上記の日本語の説明だとわかりにくいと思うので、以下に例を示します。
例えば\(\sin x\)のマクローリン展開を考える場合は、一旦
\begin{eqnarray}
\displaystyle \sin x=a_0+a_1 x+a_2 x^2+a_3 x^3+a_4 x^4+・・・・ \tag{1}
\end{eqnarray}
とおき、後で記載する方法で\(a_0, a_1, a_2, a_3, a_4, ,,,,\)を求めていくことで、\(\sin x\)を \(x\)のべき乗で表現することを考えていきます。
ポイント
(1)式の右辺は、\(x\)の無限乗(\(a_\infty x^\infty\))まで続く無限次多項式です。
■マクローリン展開の導出方法について
それでは、(1)式の\(a_0, a_1, a_2, a_3, a_4, ,,,,\)を求めていってみましょう。
、、、といっても実はそんなに難しくないです。
①\(a_0\)を求める
(1)式において、\(x=0\)を代入すると、
\begin{eqnarray}
\displaystyle 左辺&=&\sin 0=0 \\
\displaystyle 右辺&=&a_0+a_1・0+a_2・0+a_3・0+a_4・0+・・・・=a_0
\end{eqnarray}
となるため、これより、
\begin{eqnarray}
\displaystyle a_0=0 \\
\end{eqnarray}
であることがわかる。

上の手順①では、どのような\(x\)の値でも(1)式が成立するような\(a_0, a_1, a_2, a_3, a_4, ,,,,\)を求めています。
そのため、\(x=0\)の時も(1)式は成立するはずであることを利用して、\(a_0\)を求めている、というわけです。
ちなみに以下の手順②~④でも、同様の考え方を利用しています。
②\(a_1\)を求める
(1)式の両辺を\(x\)で微分すると、
\begin{eqnarray}
\displaystyle \cos x=a_1 x+2・a_2 x+3・a_3 x^2+4・a_4 x^3+・・・・ \tag{2}
\end{eqnarray}
(2)式において、\(x=0\)を代入すると、
\begin{eqnarray}
\displaystyle 左辺&=&\cos 0=1 \\
\displaystyle 右辺&=&a_1・0+2・a_2・0+3・a_3・0+4・a_4・0+・・・=a_1
\end{eqnarray}
となるため、これより、
\begin{eqnarray}
\displaystyle a_1=1 \\
\end{eqnarray}
であることがわかる。
③\(a_2\)を求める
(2)式の両辺を\(x\)で微分すると、
\begin{eqnarray}
\displaystyle -\sin x=2・a_2+2・3・a_3 x+3・4・a_4 x^2+・・・・ \tag{3}
\end{eqnarray}
(3)式において、\(x=0\)を代入すると、
\begin{eqnarray}
\displaystyle 左辺&=&-\sin 0=0 \\
\displaystyle 右辺&=&2・a_2+2・3・a_3・0+3・4・a_4・0+・・=2・a_2
\end{eqnarray}
となるため、これより、
\begin{eqnarray}
\displaystyle a_2=0 \\
\end{eqnarray}
であることがわかる。
④\(a_3\)を求める
(3)式の両辺を\(x\)で微分すると、
\begin{eqnarray}
\displaystyle -\cos x=2・3・a_3+2・3・4・a_4 x+・・・・ \tag{4}
\end{eqnarray}
(4)式において、\(x=0\)を代入すると、
\begin{eqnarray}
\displaystyle 左辺&=&-\cos 0=-1 \\
\displaystyle 右辺&=&2・3・a_3+2・3・4・a_4・0+・・・・=2・3・a_3
\end{eqnarray}
となるため、これより、
\begin{eqnarray}
\displaystyle a_3=-\frac{1}{6}=-\frac{1}{3!} \\
\end{eqnarray}
であることがわかる。
、、、なんとなくわかってきたでしょうか?つまり、「微分して」「\(x=0\)を代入」を繰り返していけば、どんどん\(a_n\)の値を求めていくことができます。
同様の操作で、\(a_4, a_5, a_6, a_7\)についても求めていくと、
\begin{eqnarray}
\displaystyle a_4&=&0 \\
\displaystyle a_5&=&\frac{1}{120}=\frac{1}{5!} \\
\displaystyle a_6&=&0 \\
\displaystyle a_7&=&-\frac{1}{5040}=-\frac{1}{7!}
\end{eqnarray}
であることがわかります。(気になる人は各自でやってみて下さい!)
これまで求めてきた\(a_0~a_7\)を(1)式に代入すると、
\begin{eqnarray}
\displaystyle \sin x&=&x-\frac{1}{3!} x^3+\frac{1}{5!} x^5-\frac{1}{7!} x^7+・・・・
\end{eqnarray}
となることがわかります。これが、マクローリン展開の基本的な考え方です。
同様の手順で、\(\cos x, e^x\)についてもマクローリン展開をしてみると、
\begin{eqnarray}
\displaystyle \cos x&=&1-\frac{1}{2!} x^2+\frac{1}{4!} x^4-\frac{1}{6!} x^6+・・・・ \\
\displaystyle e^x&=&1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\frac{1}{4!}x^4+・・
\end{eqnarray}
上式のように導出することができます。

上記3式のマクローリン展開は、実はシグマを用いて以下のようにシンプルな形に表すことができます。
※下記の形はここでは特に覚えなくて大丈夫です!
\begin{eqnarray}
\sin x &=& \displaystyle \sum_{n=0}^\infty (-1)^n\frac{1}{(2n+1)!}x^{2n+1} \\
\cos x &=& \displaystyle \sum_{n=0}^\infty (-1)^n\frac{1}{(2n)!}x^{2n} \\
e^x &=& \displaystyle \sum_{n=0}^\infty \frac{1}{n!}x^{n}
\end{eqnarray}
上の3式が成立することの証明は本記事では割愛しますが、これまでの説明で「上式が成立しそう!」というところまで理解してもらえれば一旦大丈夫です!
■【補足】マクローリン展開の数学的意味
補足として、マクローリン展開の数学的意味について簡単に説明していきます。
\(\sin x\)をマクローリン展開した式の左辺、右辺に着目します。
\begin{eqnarray}
\displaystyle \sin x&=&x-\frac{1}{3!} x^3+\frac{1}{5!} x^5-\frac{1}{7!} x^7+・・・・
\end{eqnarray}
上式の左辺を \(f(x)\) とおき、以下のように
\begin{eqnarray}
f(x)&=&\sin x
\end{eqnarray}
とおきます。
一方、右辺について \(x^5\)、\(x^7\)、\(x^9\) まで展開したものをそれぞれ \(g(x)\)、\(h(x)\)、\(p(x)\) とおくと、
\begin{eqnarray}
g(x)&=&x-\frac{1}{3!} x^3+\frac{1}{5!} x^5 \\
h(x)&=&x-\frac{1}{3!} x^3+\frac{1}{5!} x^5-\frac{1}{7!} x^7 \\
p(x)&=&x-\frac{1}{3!} x^3+\frac{1}{5!} x^5-\frac{1}{7!} x^7+\frac{1}{9!} x^9
\end{eqnarray}
と定義します。

右辺については無限次の項まで考えるのは無理なため、一旦途中までの項として、\(g(x)\)では5次まで、\(h(x)\)では7次まで、\(p(x)\)では9次までの項を考えてみてます。
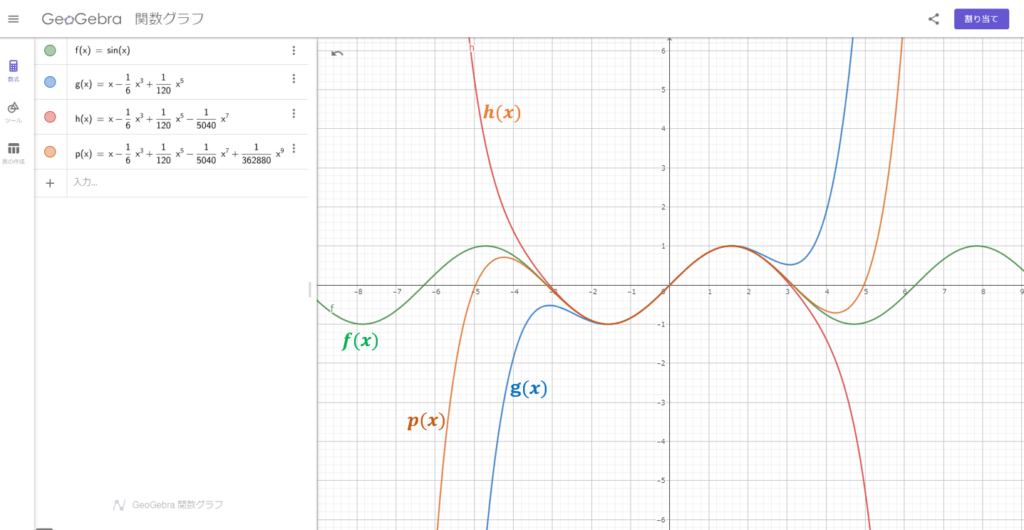
\(f(x)\)、\(g(x)\)、\(h(x)\)、\(p(x)\) の各関数についてグラフを描いてみると、それぞれ以下のようになります。
※グラフが小さいと思うので、適宜拡大してご確認ください。
※上記グラフ描写は、以下サイトのツールを使用させていただきました。
GeoGebra:<https://www.geogebra.org/graphing?lang=ja>
上のそれぞれの図を見比べてみて、いかがでしょうか?気付きますかね、、、
そう、\(g(x), h(x), p(x)\)の各グラフとも、\(x=0\) 付近で\(f(x)\)のグラフと形がほぼ一致してますよね。
また、\(g(x)\)よりも\(h(x)\)、\(h(x)\)よりも\(p(x)\)の方が、\(f(x)\)とグラフが一致している範囲が広いこともわかるかと思います。

\(g(x)\)は\(-2 \lt x \lt 2\)ぐらいの範囲までしか\(f(x)\)のグラフと一致していないのに対し、
\(p(x)\)は\(-4 \lt x \lt 4\)ぐらいの範囲まで\(f(x)\)のグラフと一致してることがわかると思います。
以上のことから、マクローリン展開の特徴について、
(1) マクローリン展開で5次までの項しか展開していない場合でも、\(x=0\) の付近の値であれば、近似としては十分な精度となる。
(2) マクローリン展開を高次の項まで考慮すればするほど、\(x=0\) の付近でなくても近似できるようになり、かつ、より高精度で\(\sin x\) の値(グラフ)に近づけることができる。
とまとめることができます。
※\(\cos x, e^x\)のマクローリン展開についても同様にまとめることができます。
最後に例として、\(f(x), g(x), h(x), p(x)\)に\(x=1\)を代入した値を見てみると、
\begin{eqnarray}
f(1)&=&0.841470985,,,,,, \\
g(1)&=&0.841666666,,,,,,(f(1)との差:0.000195681) \\
h(1)&=&0.841468254,,,,,,(f(1)との差:0.000002731) \\
p(1)&=&0.841471009,,,,,,(f(1)との差:0.000000024)
\end{eqnarray}
となり、\(x\)の高次の項まで考慮すればするほど、マクローリン展開の”近似”の精度が上がっていくことがわかります。
■オイラーの公式の導出!
これまで見てきた\(\sin x, \cos x, e^x\)のマクローリン展開を利用してオイラーの公式を導出していきます。
改めて、\(\sin x, \cos x, e^x\)のマクローリン展開を以下に記載すると、
\begin{eqnarray}
\displaystyle \sin x&=&x-\frac{1}{3!} x^3+\frac{1}{5!} x^5-\frac{1}{7!} x^7+・・ \tag{5} \\
\displaystyle \cos x&=&1-\frac{1}{2!} x^2+\frac{1}{4!} x^4-\frac{1}{6!} x^6+・・ \tag{6} \\
\displaystyle e^x&=&1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\frac{1}{4!}x^4+\frac{1}{5!}x^5+・・ \tag{7}
\end{eqnarray}
となります。
これを見て、(5)式と(6)式を足し合わせると、(7)式に近くなる、ということに皆さんも気付くかと思います。
しかし、ただ単純に足し合わせただけでは、式の形が似たものにはなりますが、一致はしません。(符号が合わない項が現れます)
ここで試しに、(7)式において、「\(x\)」の代わりに「\(ix\)」を代入し、整理してみると、
\begin{eqnarray}
\displaystyle e^{ix}&=&1+ix+\frac{1}{2!} (ix)^2+\frac{1}{3!} (ix)^3+\frac{1}{4!} (ix)^4+\frac{1}{5!} (ix)^5+・・ \\
\displaystyle &=&1+ix-\frac{1}{2!} x^2-\frac{1}{3!} ix^3+\frac{1}{4!} x^4+\frac{1}{5!} ix^5+・・ \tag{8}
\end{eqnarray}
※ただし、\(i\)は虚数単位であり、\(i^2=-1\)を利用して式変形を行っている。
(8)式であれば、(5)式と(6)式を足し合わせれば、各項の符号については一致するようになります。
しかし、(8)式の偶数番目の項については、全ての項に虚数\(i\)が掛け算されています。
以上のことから、【(5)式×\(i\)+(6)】をすることで、右辺の形が(8)式の右辺に一致するため、(5)式、(6)式、(8)式の間で以下の関係が成立します。
\begin{eqnarray}
\displaystyle e^{ix}=\cos x+i\sin x \tag{☆}
\end{eqnarray}
実は(☆)式こそが、オイラーの公式の一般形です!
(☆)式において、\(x=\pi\)を代入すると、
\begin{eqnarray}
\displaystyle e^{i\pi}=-1
\end{eqnarray}
となり、記事冒頭で表記したオイラーの公式
\begin{eqnarray}
\displaystyle e^{i\pi}+1=0
\end{eqnarray}
が導けます!
■まとめ
いかがでしたでしょうか?
何かと有名なオイラーの公式ですが、フタを開けてみればこのくらい簡単に証明ができるものなのです。
私もこの公式を大学数学で初めて勉強した時は、そもそもマクローリン展開が理解できず、苦しんだものです。
(大学では何かと小難しく数学を教えてくるので、、、)
でも振り返ってみると、高校数学のみの知識で、オイラーの公式の導出まではできましたよね!
で、この数式のすごいところは、「円周率(\(\pi\))」と「ネイピア数(\(e\))」という一見無関係な定数が、虚数(\(i\))を利用することにより、こんなに綺麗な公式で結び付けられるところにあると思っています!
こういったところから、少しでも数学の楽しさを知ってもらえれば、これ以上の喜びはありません。
ここまで記事を読んでいただき、ありがとうございました!
