【三角関数の極限公式の証明】
絶対わかるように丁寧に導出！

三角関数の極限\((\displaystyle \lim_{h \to 0} \frac{\sin h}{h} = 1)\)の証明をメチャクチャ丁寧に記述してみました。

【手順1】図形を描く

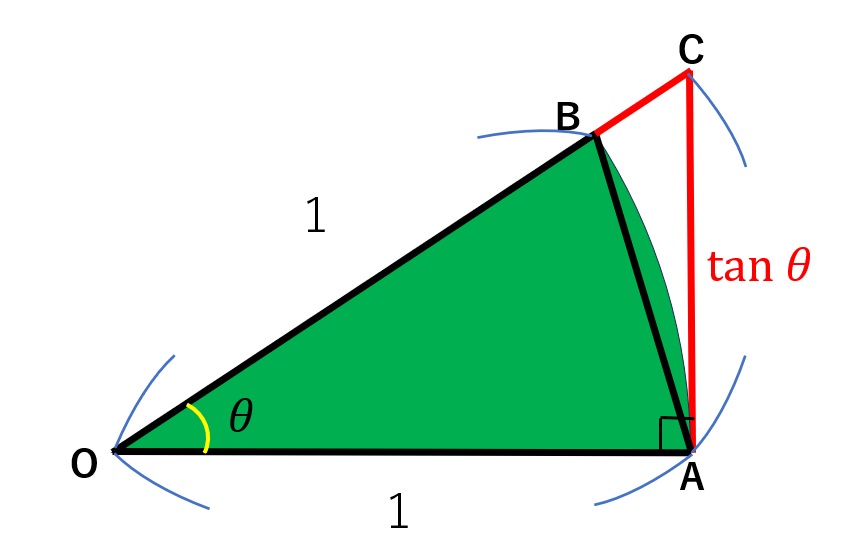
上の図を参考に描いてみてください。描き方は以下を参照。

　(1) まず半径1の扇形OABを描く。

　(2) その後、点Aから直線OAに垂直に引いた線と
　　 直線OBが交わる点をCとする。

　(3) 三角形OACを考えると、自動的に線分ACの長さは
　　 \(\tan \theta\)と定まる。
　　　※\(\tan \theta\) と定まる理由が不明な方は、別記事＜三角関数の基本＞で \(\tan \theta\) の定義から復習してみて下さい！

【手順2】3種類の図形の面積を求める

①三角形\(OAB\)の面積

　　三角形\(OAB\)の面積は【\(OA × OB × \sin \theta\)】で求められるため、

　　\(\displaystyle 1 × 1 × \frac{1}{2} × \sin \theta = \frac{1}{2}\sin \theta\)

②扇形\(OAB\)の面積

　　扇形の面積の公式（半径×半径×\(\pi×\displaystyle \frac{\theta}{2\pi}\)）より、

　　\(\displaystyle 1 × 1 × \pi × \frac{\theta}{2\pi} = \frac{1}{2}\theta\)

③三角形\(OAC\)の面積

　　三角形\(OAC\)の面積は【\(OA × AC × \displaystyle\frac{1}{2}\)】で求められるため、

　　\(\displaystyle 1 × \tan \theta × \frac{1}{2} = \frac{1}{2}\tan \theta\)

上で求めた①、②、③をまとめると、

三角形\(OAB\)の面積： \(\displaystyle\frac{1}{2}\sin \theta\)
扇形\(OAB\)の面積： \(\displaystyle\frac{1}{2}\theta\)、　
三角形\(OAC\)の面積： \(\displaystyle\frac{1}{2}\tan \theta\)

【手順3】求めた面積の大小関係を比較する

手順1にて描いた図形より、[三角形\(OAB\)] < [扇形\(OAB\)] < [三角形\(OAC\)]が明らかなため、

\begin{eqnarray}
\frac{1}{2}\sin \theta < \frac{1}{2}\theta < \frac{1}{2}\tan \theta \tag{1}
\end{eqnarray}

各辺に \(\times \displaystyle\frac{2}{\sin \theta}\)をすると、

\begin{eqnarray}
1 < \frac{\theta}{\sin \theta} < \frac{1}{\cos \theta} \tag{2}
\end{eqnarray}

両辺の分母と分子を入れ替えると、（※この操作では不等号の向きが変わることに注意）

\begin{eqnarray}
1 > \frac{\sin \theta}{\theta} > \cos \theta \tag{3}
\end{eqnarray}

【手順4】\(\theta\)→0 の極限を考え、はさみうちの原理を使う

(3)式の各辺において、\(\theta\)→0の極限を考えると、

\begin{equation}
\displaystyle \lim_{\theta \to 0} 1 > \displaystyle \lim_{\theta \to 0} \frac{\sin \theta}{\theta} > \displaystyle \lim_{\theta \to 0} \cos \theta \tag{4}
\end{equation}

\begin{equation}
1 > \displaystyle \lim_{\theta \to 0} \frac{\sin \theta}{\theta} > 1 \tag{5}
\end{equation}

　※もし \(\displaystyle \lim_{\theta \to 0} \cos \theta\) となる理由が不明な方は、別記事＜三角関数の基本＞で \(\cos \theta\) の定義を確認してみて下さい！

(5)式において、「 \(\displaystyle \lim_{\theta \to 0} \frac{\sin \theta}{\theta}\) は1以上かつ1以下の値を取る」、ということになるため、結果としてこの値は

\begin{eqnarray}
\displaystyle \lim_{\theta \to 0} \frac{\sin \theta}{\theta} = 1 \tag{6}
\end{eqnarray}

と定まる。
　※学校では「はさみうちの原理」と習う部分だと思います。

最後に、(6)式の\(\theta\)を\(h\)に入れ替えると、証明したい式を得る。

【おまけ】FAQ

今回\(\displaystyle \lim_{h \to 0} \frac{\sin h}{h} = 1\)を証明していますが、\(\displaystyle \lim_{h \to 0} \frac{h}{\sin h} = 1\)は成立するのでしょうか？

成立します。(2)式の各辺において、\(\theta\)→0の極限を考えると得られます。

本サイトでは\(0^{ \circ }< \theta < 90^{ \circ }\)として証明しているため、正確には
\(\displaystyle \lim_{h \to +0} \frac{\sin h}{h} = 1\)の証明がされただけではないでしょうか？
　⇒言い換えると、\(\displaystyle \lim_{h \to -0} \frac{\sin h}{h} = 1\)の証明もする必要があるんじゃないでしょうか？

ご指摘の通りです。（簡潔さを優先するため、省略しました）
\(h\)をマイナスから0に近づけた時の値については、以下のように考えます。
\begin{equation}
\displaystyle \lim_{h \to -0} \frac{\sin h}{h}
\end{equation}
ここで、\(h=-t\)と変換すると、
\begin{equation}
=\displaystyle \lim_{t \to +0} \frac{\sin (-t)}{(-t)}
\end{equation}
\(\sin(-t)=-\sin t\)より、
\begin{equation}
=\displaystyle \lim_{t \to +0} \frac{\sin t}{t}
\end{equation}
となるので結局、\(h\)をプラスから0に近づけた時の値と一致します。