本記事では、高校生で習う三角関数の以下の加法定理が何故成り立つのか、できるだけ丁寧にまとめてみました！
是非参考にしていただけると幸いです！
上式の証明は、以下の手順で行っていきます！
）証明手順
①\(\cos(\alpha-\beta)\)を証明する
②\(\cos(\alpha+\beta)\)を証明する
③\(\cos(90^{ \circ }-\theta)=\sin\theta\), \(\sin(90^{ \circ }-\theta)=\cos\theta\) を証明する
（※次手順で利用するため）
④「③」を利用して、\(\sin(\alpha+\beta)\)を証明する
⑤ \(\displaystyle \tan\theta=\frac{\sin\theta}{\cos\theta}\) より、\(\tan(\alpha+\beta)\)を証明する
見出し
- ■証明手順①：\(\cos(\alpha-\beta)\) の値を求める
- ■証明手順②：\(\cos(\alpha+\beta)\) の値を求める
- ■証明手順③：\(\cos(90^{ \circ }-\theta)=\sin\theta\)、\(\sin(90^{ \circ }-\theta)=\cos\theta\) を図から証明する
- ■証明手順④：「③」を利用して、\(\sin(\alpha+\beta)\) の値を求める
- ■証明手順⑤：\(\displaystyle \tan\theta=\frac{\sin\theta}{\cos\theta}\) より、\(\tan(\alpha+\beta)\) の値を求める
- ■まとめ
■証明手順①：\(\cos(\alpha-\beta)\) の値を求める
以下の図から、視覚的に簡単に証明できます。
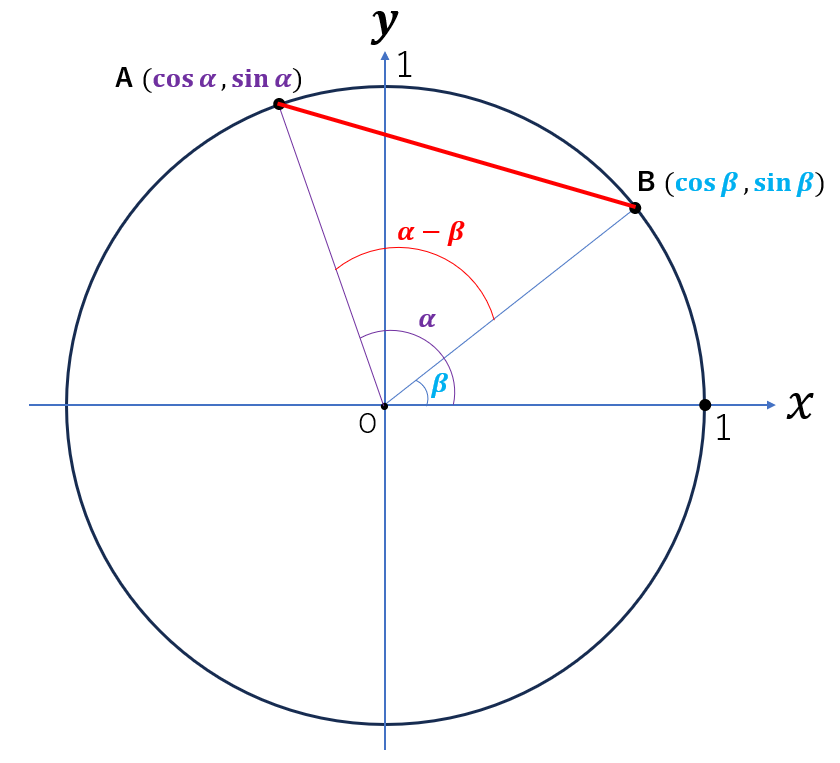
上図の線分ABの長さを2通りの方法で考えることで、加法定理を証明する。
(a) 座標成分で三平方の定理を利用し、線分\(AB^2\)を求める
(b) 余弦定理（\(AB^2=OA^2+OB^2-2\cos(\alpha-\beta)\)）で線分\(AB^2\)を求める
(a) 座標成分で線分\(AB^2\)を求める
\begin{eqnarray}
AB^2 &=& (\cos\alpha - \cos\beta)^2+(\sin\alpha - \sin\beta)^2 \\
&=& (\cos^2\alpha - 2\cos\alpha\cos\beta + \cos^2\beta) \\
& &+(\sin^2\alpha - 2\sin\alpha\sin\beta + \sin^2\beta) \\
&=& (1 - 2\cos\alpha\cos\beta)+(1 - 2\sin\alpha\sin\beta) \\
&=& 2 - 2(\cos\alpha\cos\beta+\sin\alpha\sin\beta) \tag{1}
\end{eqnarray}
(b) 余弦定理（\(AB^2=OA^2+OB^2-2\cos(\alpha-\beta)\)）で線分\(AB^2\)を求める
\begin{eqnarray}
AB^2 &=& OA^2+OB^2-2\cos(\alpha-\beta) \\
&=& 1+1-2\cos(\alpha-\beta) \\
&=& 2 - 2\cos(\alpha-\beta) \tag{2}
\end{eqnarray}
(1)式、(2)式を比較すると、
\[2 - 2(\cos\alpha\cos\beta+\sin\alpha\sin\beta) = 2 - 2\cos(\alpha-\beta)\]
となるため、この式より、
\[\cos(\alpha-\beta) = \cos\alpha\cos\beta+\sin\alpha\sin\beta\]
を得る。
もし「余弦定理って何？」という方がいたら、こちらのリンクに説明記事があるので、よろしければ併せて参照してみて下さい！
■証明手順②：\(\cos(\alpha+\beta)\) の値を求める
これは、\(\cos(\alpha+\beta) = \cos(\alpha-(-\beta))\)を利用するだけである。
さっき証明した加法定理（\(\cos(\alpha-\beta) = \cos\alpha\cos\beta+\sin\alpha\sin\beta\)）の公式を利用して、
\begin{eqnarray}
\cos(\alpha+\beta) &=& \cos(\alpha-(-\beta)) \\
&=& \cos\alpha\cos(-\beta)+\sin\alpha\sin(-\beta) \\
&=& \cos\alpha\cos\beta-\sin\alpha\sin\beta \\
\end{eqnarray}
となり、まず\(\cos\)の加法定理が証明できる。
※ただし、上の式変形では \(\cos(-\beta)=\cos\beta, \sin(-\beta)=-\sin\beta\) を利用した。
上の赤マーカー部分の式変形がよくわからない、、、という方は、こちらのリンクに説明記事があるので、よろしければ併せて参照してみて下さい！
■証明手順③：\(\cos(90^{ \circ }-\theta)=\sin\theta\)、\(\sin(90^{ \circ }-\theta)=\cos\theta\) を図から証明する
ここで少しずれるが、この後の手順で \(\cos(90^{ \circ }-\theta)=\sin\theta\) と \(\sin(90^{ \circ }-\theta)=\cos\theta\) を使うため、証明しておく。
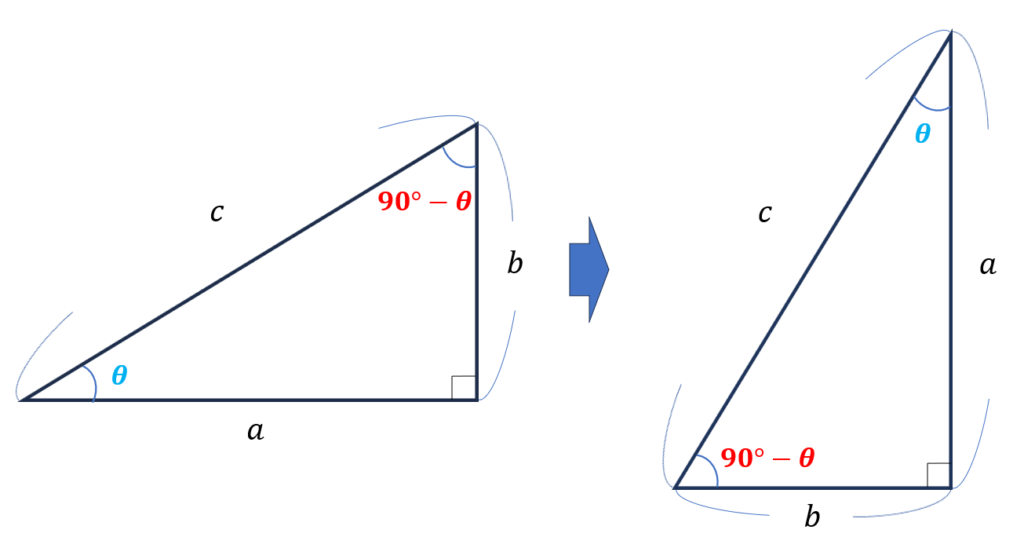
上の２つの三角形は合同の三角形であり、少し向きを変えただけのものである。
左の三角形より、\(\sin\theta, \cos\theta\) はそれぞれ
\begin{eqnarray}
\displaystyle \sin\theta = \frac{b}{c} \tag{3} \\
\displaystyle \cos\theta = \frac{a}{c} \tag{4}
\end{eqnarray}
で表される。
一方、右の三角形より、\(\sin(90^{ \circ }-\theta), \cos(90^{ \circ }-\theta)\)はそれぞれ
\begin{eqnarray}
\displaystyle \sin(90^{ \circ }-\theta) = \frac{a}{c} \tag{5} \\
\displaystyle \cos(90^{ \circ }-\theta) = \frac{b}{c} \tag{6}
\end{eqnarray}
と表されるので、あとは(3)式と(6)式、(4)式と(5)式の右辺が等しいことから、
\begin{eqnarray}
\displaystyle \sin(90^{ \circ }-\theta) = \cos\theta \\
\displaystyle \cos(90^{ \circ }-\theta) = \sin\theta
\end{eqnarray}
が証明される。
■証明手順④：「③」を利用して、\(\sin(\alpha+\beta)\) の値を求める
先ほど証明した、\(\cos(90^{ \circ }-\theta) = \sin\theta\)、\(\sin(90^{ \circ }-\theta) = \cos\theta\)を利用すると、
\begin{eqnarray}
\displaystyle \sin(\alpha+\beta) &=& \cos(90^{ \circ }-(\alpha+\beta)) \\
\displaystyle &=& \cos((90^{ \circ }-\alpha)-\beta) \\
\displaystyle &=& \cos(90^{ \circ }-\alpha)\cos\beta \\
& &+\sin(90^{ \circ }-\alpha)\sin\beta \\
\displaystyle &=& \sin\alpha\cos\beta+\cos\alpha\sin\beta
\end{eqnarray}
となり、\(\sin\)の加法定理が証明できる。
■証明手順⑤：\(\displaystyle \tan\theta=\frac{\sin\theta}{\cos\theta}\) より、\(\tan(\alpha+\beta)\) の値を求める
さあ、最後です。
公式\(\displaystyle \tan\theta=\frac{\sin\theta}{\cos\theta}\)を利用すると、
\begin{eqnarray}
\displaystyle \tan(\alpha+\beta) &=& \frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)} \\
\displaystyle &=& \frac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta} \tag{7} \\
\end{eqnarray}
(7)式の分母分子を \(\cos\alpha\cos\beta\) で割ると、
\begin{eqnarray}
\tan(\alpha+\beta) &=& \frac{\frac{\sin\alpha\cos\beta}{\cos\alpha\cos\beta}+\frac{\cos\alpha\sin\beta}{\cos\alpha\cos\beta}}{1-\frac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}} \\
\displaystyle &=& \frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta} \tag{8}
\end{eqnarray}
となり、\(\tan\)の加法定理も証明ができる。
■まとめ
いかがでしたでしょうか？
振り返ってみれば、\(\cos(a-b)\)さえ証明することができれば、加法定理を芋づる式に証明することができることがわかると思います。
■加法定理の証明手順（おさらい）
①\(\cos(a-b)\)を証明する
↓
②\(\cos(a+b)\)を証明する
↓
③\(\sin(a+b)\)を証明する
↓
④\(\tan(a+b)\)を証明する
こういった公式は語呂合わせで覚えるだけではなく、いつでも証明できる状態で使用できたほうが数学がもっと面白くなると思いますので、是非是非この機会に覚えていってもらえたら幸いです！
ここまで本記事を読んでいただき、ありがとうございました！